461. 汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
题解
class Solution {
public:
// // 使用内置函数统计1的个数
// int hammingDistance(int x, int y) {
// return __builtin_popcount(x^y);
// }
// // 使用移位统计1的个数
// int hammingDistance(int x, int y) {
// int res = 0;
// int s = x^y;
// while(s){
// res += s&1;
// s >>= 1;
// }
// return res;
// }
// 利用s&s-1可以消去一个1来统计1的个数
int hammingDistance(int x, int y) {
int res = 0;
int R = 1;
int s = x^y;
while(s){
s = s&(s-1);
res++;
}
return res;
}
};
448. 找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
输入:nums = [4,3,2,7,8,2,3,1]
输出:[5,6]
输入:nums = [1,1]
输出:[2]
题解
这一类题三种方法:交换位置,赋值为相反数,统一增加n
相似的题:找到数组中重复的数
class Solution {
public:
// 方法1:交换到对应位置上去,注意数值要减1,因为数从1开始,索引从0开始
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> res;
int n = nums.size();
for(int i = 0; i < n; ++i){
while(nums[nums[i] - 1] != nums[i])
swap(nums[nums[i] - 1], nums[i]);
}
for(int i = 0; i < n; ++i){
if(nums[i]-1 != i)
res.push_back(i+1);
}
return res;
}
// // 方法2:赋值为相反数
// vector<int> findDisappearedNumbers(vector<int>& nums) {
// vector<int> res;
// int n = nums.size();
// for(int i = 0; i < n; ++i){
// int idx = abs(nums[i])-1;
// nums[idx] = -abs(nums[idx]); //所有出现的数字对应的索引的值都为负数
// }
// for(int i = 0; i < n; ++i){
// if(nums[i] > 0)
// res.push_back(i+1);
// }
// return res;
// }
// // 方法3:统一增加长度n
// vector<int> findDisappearedNumbers(vector<int>& nums) {
// vector<int> res;
// int n = nums.size();
// for(int i = 0; i < n; ++i){
// int idx = nums[i]-1;
// nums[idx%n] += n; // 所有出现的数字对应的索引的值的大小都大于n
// }
// for(int i = 0; i < n; ++i){
// if(nums[i] <= n)
// res.push_back(i+1);
// }
// return res;
// }
};
494. 目标和
给你一个整数数组 nums和一个整数 target 。向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
题解
似乎是背包问题,可以查看一下
class Solution {
public:
// // 暴力回溯法。复杂度2^n
// void backtrack(vector<int>& nums, int s, int idx, int &res){
// if(idx == nums.size()){
// res += (s == 0);
// return;
// }
// backtrack(nums, s+nums[idx], idx+1, res);
// backtrack(nums, s-nums[idx], idx+1, res);
// }
// int findTargetSumWays(vector<int>& nums, int target) {
// int res = 0;
// backtrack(nums, target, 0, res);
// return res;
// }
// 记忆化数组方法
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size();
vector<unordered_map<int,int>> dp(n+1);
dp[0][0] = 1;
for(int i = 0; i < n; ++i){
// 理解一下这里
for(auto&a : dp[i]){
int sum = a.first, cnt = a.second;
dp[i+1][sum+nums[i]] += cnt;
dp[i+1][sum-nums[i]] += cnt;
}
}
return dp[n][target];
}
};
543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 递归获取最大直径,并返回该节点的深度,方便上一层使用
int diameter(TreeNode* root, int &res){
if(!root)
return 0;
int l = diameter(root->left, res);
int r = diameter(root->right, res);
res = max(res, l+r);
return max(l, r)+1;
}
int diameterOfBinaryTree(TreeNode* root) {
int res = 0;
diameter(root, res);
return res;
}
};
560. 和为K的子数组
给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
输入:nums = [1,1,1], k = 2
输出:2, [1,1] 与 [1,1] 为两种不同的情况。
题解
class Solution {
public:
// // 暴力解法,O(n^2),无法通过测试
// int subarraySum(vector<int>& nums, int k) {
// int n = nums.size();
// int count = 0;
// for(int i = 0; i < n; ++i){
// int sum = 0;
// for(int j = i; j >= 0; --j){ // 这里还是得想一下
// sum += nums[j];
// if(sum == k)
// count++;
// }
// }
// return count;
// }
// 用一个哈希表记录前缀和出现的次数,具体看题解
int subarraySum(vector<int>& nums, int k) {
int n = nums.size();
int count = 0;
unordered_map<int, int> m;
m[0] = 1; // 初始化0为1是为了当nums[i]刚好为k的时候也能使得count加1
int pre = 0;
for(int i = 0; i < n; ++i){
pre += nums[i];
auto it = m.find(pre-k);
if(it != m.end())
count += it->second;
m[pre]++;
}
return count;
}
};
581. 最短无序连续子数组
给你一个整数数组 nums ,你需要找出一个连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。请你找出符合题意的 最短子数组,并输出它的长度。
输入:nums = [2,6,4,8,10,9,15]
输出:5
解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
输入:nums = [1,2,3,4]
输出:0
题解
class Solution {
public:
// //暴力法:对每一个i,若i-n之间存在j使得n[j]<n[i],那么说明i, j之间不是有序的,那么找到最小的i和最大的j即可。
// int findUnsortedSubarray(vector<int>& nums) {
// int n = nums.size();
// int l = n, r = 0;
// for(int i = 0; i < n; ++i){
// for(int j = i+1; j < n; ++j){
// if(nums[j] < nums[i]){
// l = min(l, i);
// r = max(r, j);
// }
// }
// }
// return (l > r) ? 0 : r-l+1;
// }
// // 也是找最小的i和j,不过是先排序再找,这样复杂度为O(nlogn)
// int findUnsortedSubarray(vector<int>& nums) {
// int n = nums.size();
// vector<int> t(nums.begin(), nums.end());
// sort(t.begin(), t.end());
// int l = n, r = 0;
// for(int i = 0; i < n; ++i){
// if(nums[i] != t[i]){
// l = i;
// break;
// }
// }
// for(int i = n-1; i >= 0; --i){
// if(nums[i] != t[i]){
// r = i;
// break;
// }
// }
// return (l > r) ? 0: r-l+1;
// }
// // 使用栈,找到无序最小边界和最大边界
// int findUnsortedSubarray(vector<int>& nums) {
// int n = nums.size();
// stack<int> s;
// stack<int> t;
// // s.push(0);
// int l = n, r = 0;
// for(int i = 0; i < n; ++i){
// while(!s.empty() && nums[i] < nums[s.top()]){
// l = min(s.top(), l);
// s.pop();
// }
// s.push(i);
// }
// for(int i = n-1; i >= 0; --i){
// while(!t.empty() && nums[i] > nums[t.top()]){
// r = max(t.top(), r);
// t.pop();
// }
// t.push(i);
// }
// return (l > r) ? 0: r-l+1;
// }
// 仅需遍历一次,找到无序最小边界和最大边界,和上面栈的方式类似
int findUnsortedSubarray(vector<int>& nums) {
int n = nums.size();
int l = -1, r = -2;
int big = nums[0], small = nums[n-1];
for(int i = 1; i < n; ++i){
if(big > nums[i]) r = i;
else big = nums[i];
if(small < nums[n-i-1]) l = n-i-1;
else small = nums[n-i-1];
}
return r-l+1;
}
};
617. 合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/ \
4 5
/ \ \
5 4 7
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(!root2)
return root1;
if(!root1){
return root2;
}
TreeNode* head = root1;
head->val = root1->val+root2->val;
head->left = mergeTrees(root1->left, root2->left);
head->right = mergeTrees(root1->right, root2->right);
return head;
}
};
647. 回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
输入:"abc"
输出:3
解释:三个回文子串: "a", "b", "c"
输入:"aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
题解
class Solution {
public:
// bool isSub(string& s, int i, int j){
// for(int p = i, q = j; p < q; p++, q--){
// if(s[p] != s[q])
// return false;
// }
// return true;
// }
// // 暴力法,对每一个子串,判断是不是回文子串,但这是O(n^3)复杂度
// int countSubstrings(string s) {
// int n = s.length();
// int res = 0;
// for(int i = 0; i < n; ++i){
// for(int j = 0; j < n-i; ++j){
// if(isSub(s, j, j+i))
// res++;
// }
// }
// return res;
// }
// // 动态规划,dp[i][j]表示子串i-j是不是回文串
// int countSubstrings(string s) {
// int n = s.length();
// int res = 0;
// vector<vector<int>> dp(n, vector<int>(n, 0));
// for(int j = 0; j < n; ++j){
// for(int i = 0; i <= j; ++i){
// if(s[i] == s[j] && (j-i <= 2 || dp[i+1][j-1]))
// dp[i][j] = 1;
// res += dp[i][j];
// }
// }
// return res;
// }
// 中心展开来判断,是O(n^2)复杂度
void isSub(string& s, int i, int j, int &res){
while(i >= 0 && j < s.size()){
if(s[i] != s[j])
break;
res++;
i--;
j++;
}
}
int countSubstrings(string s) {
int n = s.length();
int res = 0;
for(int i = 0; i < n; ++i){
isSub(s, i, i, res);
isSub(s, i, i+1, res);
}
return res;
}
};
还有一个马拉车算法,没有弄懂,有时间再看一下吧。
739. 每日温度
请根据每日气温列表,重新生成一个列表。对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用 0 来代替。例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
题解
class Solution {
public:
// // 暴力法,用一个pos数组记录每个温度出现的最小下标,从右往左遍历,对每个温度,向右找到比他高的第一个温度出现的位置
// vector<int> dailyTemperatures(vector<int>& temperatures) {
// int n = temperatures.size();
// vector<int> res(n, 0);
// vector<int> pos(101, INT_MAX);
// for(int i = n-1; i >= 0; --i){
// int index = INT_MAX;
// for(int j = temperatures[i]+1; j <= 100; ++j){
// index = min(index, pos[j]);
// }
// if(index != INT_MAX)
// res[i] = index-i;
// pos[temperatures[i]] = i;
// }
// return res;
// }
// 单调栈(栈保存的是温度的下标),栈底到栈订是递减的,每次遍历到一个温度,若大于栈顶,则弹出,并更新栈顶对应的等待天数
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
stack<int> s;
vector<int> res(n, 0);
for(int i = 0; i < n; ++i){
while(!s.empty() && temperatures[i] > temperatures[s.top()]){
res[s.top()] = i-s.top();
s.pop();
}
s.push(i);
}
return res;
}
};
类似题:接雨水,柱状图最大矩形
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
题解
class Solution {
public:
// // 动态规划
// int trap(vector<int>& height) {
// int res = 0;
// int n = height.size();
// if(n == 0) return res;
// vector<int> leftMax(n,0);
// vector<int> rightMax(n,0);
// leftMax[0] = height[0]; // 表示i及其左边位置水能达到的最大高度
// rightMax[n-1] = height[n-1]; // 表示i及其右边位置水能达到的最大高度
// for(int i = 1; i < n; ++i)
// leftMax[i] = max(leftMax[i-1], height[i]);
// for(int i = n-2; i >= 0; --i)
// rightMax[i] = max(rightMax[i+1], height[i]);
// for(int i = 0; i < n; ++i){
// res += min(leftMax[i], rightMax[i]) - height[i]; // 位置i能接的最大水量
// }
// return res;
// }
// // 单调栈:栈中元素递减,栈顶为top,次顶为left,则height[left]>height[top]
// // 当height[i]>height[top]时,我们便得到了一个能接雨水的区域,栈顶出栈,left成为新的栈顶
// int trap(vector<int>& height) {
// int res = 0;
// int n = height.size();
// stack<int> s;
// for(int i = 0; i < n; ++i){
// while(!s.empty() && height[i] > height[s.top()]){
// int t = s.top();
// s.pop();
// if(s.empty()) break;
// int left = s.top();
// int width = i-left-1; // 能接雨水宽度
// int h = min(height[left], height[i])-height[t]; // 能接雨水高度
// res += width * h;
// }
// s.push(i);
// }
// return res;
// }
// 双指针:需要好好看看题解理解一下
int trap(vector<int>& height) {
int res = 0;
int n = height.size();
int left = 0, right = n-1;
// 注意leftMax表示的是left及其左边的雨水最大高度,rightMax同理
int leftMax = 0, rightMax = 0;
while(left < right){
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);
// 如果height[left]<height[right],则left指针向右移动,因为此时leftMax,left,right形成了一个窗口
// 反之,则right指针向左移动,因为此时left,right,rightMax形成了一个窗口
if(height[left] < height[right]){
res += leftMax - height[left++];
}
else
res += rightMax - height[right--];
}
return res;
}
};
84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。
; 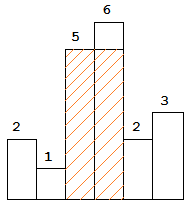
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
输入: [2,1,5,6,2,3]
输出: 10
题解
class Solution {
public:
// // 暴力动态规划, 或者直接两次循环遍历也可
// int largestRectangleArea(vector<int>& heights) {
// int res = 0;
// int n = heights.size();
// vector<vector<int>> dp(n, vector<int>(n,0));
// for(int i = 0; i < n; ++i){
// dp[i][i] = heights[i];
// res = max(res, dp[i][i]);
// for(int j = i+1; j < n; ++j){
// dp[i][j] = min(dp[i][j-1],heights[j]);
// res = max(res, dp[i][j]*(j-i+1));
// }
// }
// return res;
// }
// 单调栈
int largestRectangleArea(vector<int>& heights) {
int res = 0;
int n = heights.size();
// left和right数组表示i左右两侧第一个小于heights[i]的位置,那么对于i来说,面积就是(right[i]-left[i]-1) * heights[i]
// 所以只要知道left和right数组的值即可得到最大面积
// 而求left和right的过程就可以用单调栈来进行了
vector<int> left(n, 0), right(n, 0);
stack<int> s;
for(int i = 0; i < n; ++i){
// 注意这里是小于等于,不是单纯的小于,因为我们要找的是严格小于heights[i]的位置
while(!s.empty() && heights[i] <= heights[s.top()])
s.pop();
left[i] = (s.empty()) ? -1 : s.top();
s.push(i);
}
s = stack<int>();
for(int i = n-1; i >= 0; --i){
while(!s.empty() && heights[i] <= heights[s.top()])
s.pop();
right[i] = (s.empty()) ? n : s.top();
s.push(i);
}
for(int i = n-1; i >= 0; --i){
int area = (right[i]-left[i]-1) * heights[i];
res = max(res, area);
}
return res;
}
// // 单调栈进一步优化,仅需遍历一遍,看看题解就可以
// int largestRectangleArea(vector<int>& heights) {
// int res = 0;
// int n = heights.size();
// vector<int> left(n, 0), right(n, n);
// stack<int> s;
// for(int i = 0; i < n; ++i){
// while(!s.empty() && heights[i] <= heights[s.top()]){
// right[s.top()] = i; // 这里直接更新right数组
// s.pop();
// }
// left[i] = (s.empty()) ? -1 : s.top();
// s.push(i);
// }
// for(int i = n-1; i >= 0; --i){
// int area = (right[i]-left[i]-1) * heights[i];
// res = max(res, area);
// }
// return res;
// }
// // 单调栈空间优化
// int largestRectangleArea(vector<int>& heights) {
// int res = 0;
// int n = heights.size();
// stack<int> s;
// heights.push_back(0);
// for(int i = 0; i < n+1; ++i){
// // 注意理解一下这里
// while(!s.empty() && heights[i] <= heights[s.top()]){
// int cur = s.top();s.pop();
// int w = i;
// if(!s.empty())
// w = i-s.top()-1;
// int area = heights[cur]*w;
// res = max(res, area);
// }
// s.push(i);
// }
// return res;
// }
};